P8: The ideas of singular things, or of modes, that do not exist must be comprehended in God/Nature’s infinite idea in the same way as the formal essences of the singular things, or modes, are contained in God/Nature’s attributes.

Dem.: This Proposition is evident from the preceding one, but is understood more clearly from the preceding scholium.

Cor.: From this it follows that so long as singular things do not exist, except insofar as they are comprehended in God/Nature’s attributes, their objective being, or ideas, do not exist except insofar as God/Nature’s infinite idea exists. And when singular things are said to exist, not only insofar as they are comprehended in God/Nature’s attributes, but insofar also as they are said to have duration, their ideas also involve the existence through which they are said to have duration.

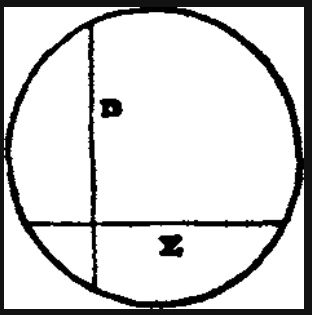
Schol.: If anyone wishes me to explain this further by an example, I will, of course, not be able to give one which adequately explains what I speak of here, since it is unique. Still I shall try as far as possible to illustrate the matter: the circle is of such a nature that the rectangles formed from the segments of all the straight lines intersecting in it are equal to one another. So in a circle there are contained infinitely many rectangles that are equal to one another. Nevertheless, none of them can be said to exist except insofar as the circle exists, nor also can the idea of any of these rectangles be said to exist except insofar as it is comprehended in the idea of the circle. Now of these infinitely many {rectangles} let two only, viz. {those formed from the segments of lines}16 D and E, exist. Of course their ideas also exist now, not only insofar as they are only comprehended in the idea of the circle, but also insofar as they involve the existence of those rectangles. By this they are distinguished from the other ideas of the other rectangles.